I enjoy word puzzles from time to time, like NYT Connections. It is a game where you try to group 16 words into 4 groups of 4, each with different themes. There are 4 difficulties of themes, easiest -> hardest.

Below is an example:

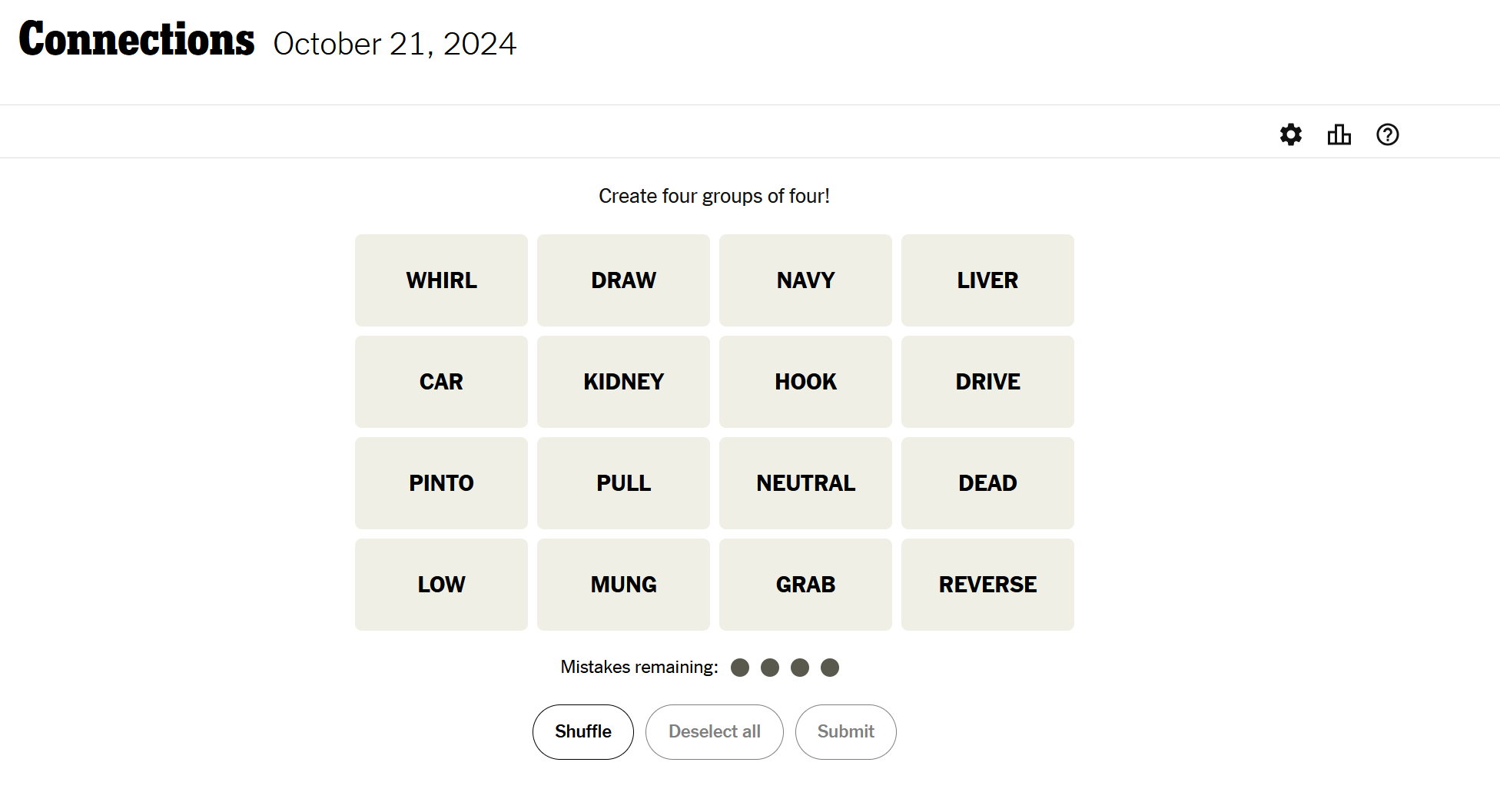
Start of NYT Connections Game for 10/21/2024

You are given 4 tries to group the 16 words above. For the example above, here are examples of the groups and themes.

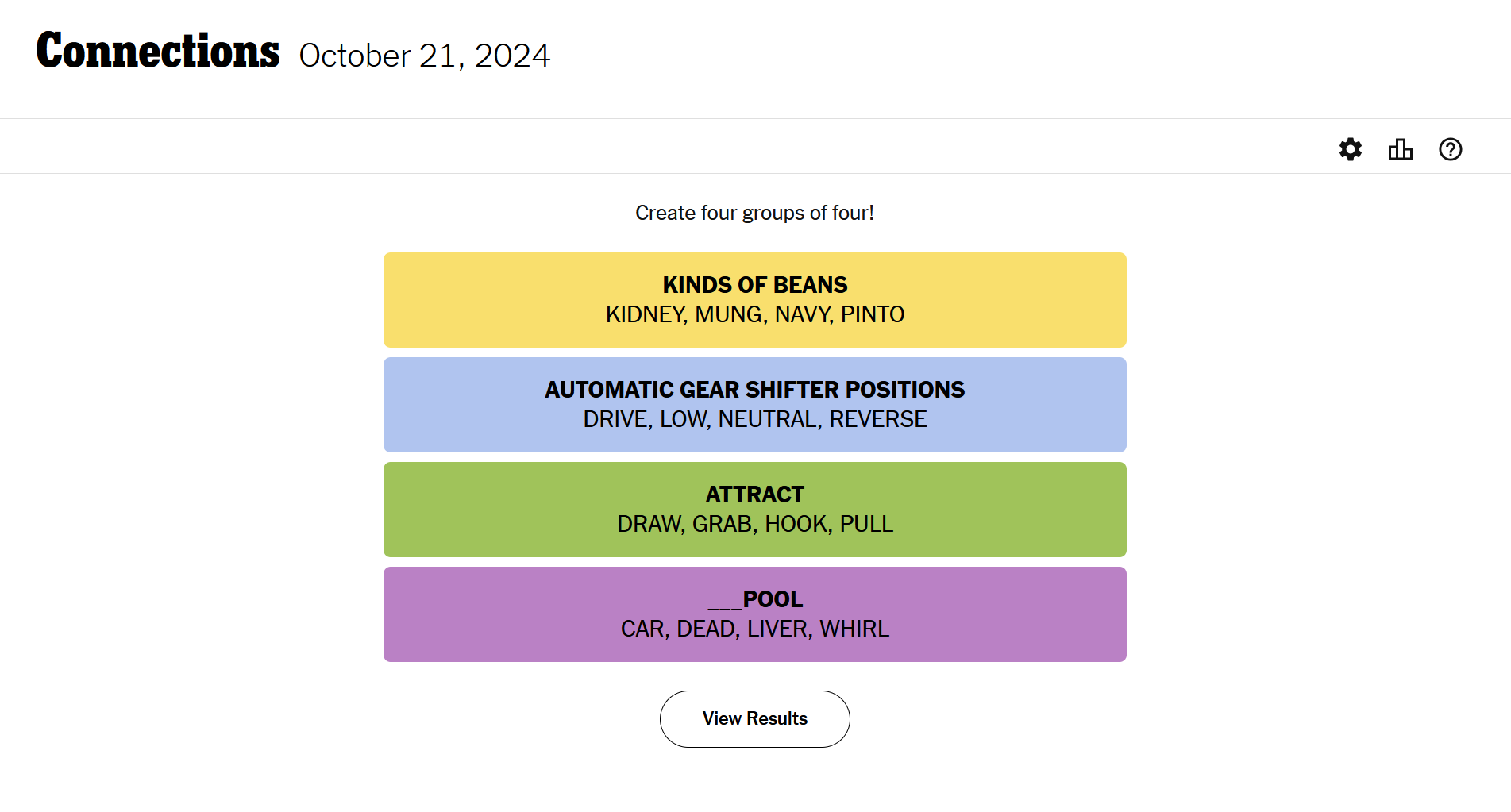
Completed NYT Connections Game for 10/21/2024

I wanted to know if NYT Connections could be solved by machines. This blog is a first attempt at “solving” the game

Experiment

I decided to frame this problem as a generative one, where the model is used to generate a structured output that indicates which words are grouped together. There are other framings, such as similarity or multi-step classification. This framing was chosen since it seemed like a strong and easy to implement baseline. The following subsections explore the setup of the experiments and different design decisions.

The code used to run the experiments can be found here.

Dataset

This repo by “Eyefyre” was used. It automatically updates through Github Actions, which saved me the effort of building a pipeline and a way of updating it regularly. Rather than continuously update the dataset, I cloned the repo on the 12th and have not updated it since. Future attempts will likely used an updated version of the dataset frozen at a later date.

Design Decisions

Not Turn-based

This version is not turn based, rather the model has a single shot to find all 4 groups. While a turn-based approach could be interesting (it enables for use of multi-turn strategies and self-correction), I’ve decided to ignore it for now to simplify things.

Quantization

4 byte quantization was used to fit even the larger models on GPU (mobile RTX 4090). The code can be run using other quantization settings (8 bit and half precision), but currently that hasn’t been done on a large scale due to time constraints.

Sample Size

Some of the larger models, especially if not quantized, don’t fit on a mobile RTX 4090 and overall run times can take up to a day for a single experiment. A sample size of 50 reduced max run times to 3-4 hours which made the experiments run in a reasonable amount of time.

Seed

Fixed seeds were set for pretty much all random operations such as shuffle and passed in a seed wherever possible. Currently all operations use the same seed, though that may change to enable for multiple generation seeds.

The seed was 42, because 42.

Output Structure

Used JSON as the output’s structure as it is easy to work with and validate using regexes/other programming tools. This may well effect impact performance in a way that makes comparing models difficult, but there likely would be no “fair” format. Here is a function which generates regex describing an example valid output,

Click to see code 
def generate_validation_regex(words):
    qouted_words = [f"\"{word}\"" for word in words]
    words_regex = f"({'|'.join(qouted_words)})"

    backreference_terms = [""] + ["(?!{})".format("".join(["\\{}".format(j) for j in range(1, i+1)])) for i in range(1, 16)]

    regex_str = r'\[\s*{{\s*"words"\s*:\s*\[\s*{words}\s*,\s*{back1}{words}\s*,\s*{back2}{words}\s*,\s*{back3}{words}\s*\]\s*,\s*"theme"\s*:\s*"[^"]*"\s*}}\s*,\s*{{\s*"words"\s*:\s*\[\s*{back4}{words}\s*,\s*{back5}{words}\s*,\s*{back6}{words}\s*,\s*{back7}{words}\s*\]\s*,\s*"theme"\s*:\s*"[^"]*"\s*}}\s*,\s*{{\s*"words"\s*:\s*\[\s*{back8}{words}\s*,\s*{back9}{words}\s*,\s*{back10}{words}\s*,\s*{back11}{words}\s*\]\s*,\s*"theme"\s*:\s*"[^"]*"\s*}}\s*,\s*{{\s*"words"\s*:\s*\[\s*{back12}{words}\s*,\s*{back13}{words}\s*,\s*{back14}{words}\s*,\s*{back15}{words}\s*\]\s*,\s*"theme"\s*:\s*"[^"]*"\s*}}\s*\]'.format(words=words_regex,
        back1=backreference_terms[1], back2=backreference_terms[2], back3=backreference_terms[3],
        back4=backreference_terms[4], back5=backreference_terms[5], back6=backreference_terms[6], back7=backreference_terms[7],
        back8=backreference_terms[8], back9=backreference_terms[9], back10=backreference_terms[10], back11=backreference_terms[11],
        back12=backreference_terms[12], back13=backreference_terms[13], back14=backreference_terms[14], back15=backreference_terms[15]
    )

    return regex_str.strip()

The gist of it is that words is generated from a fixed set and words can’t repeat (hence the lookarounds, see back1->back15).

Guided Generation

For guided generation Outlines and a Pydantic data model. I couldn’t figure out how to add a condition to Pydantic to limit generation for words to one instances. Consets don’t appear supported by Outlines and I kept getting a “can’t be hashed” error.

Later I wrote a regex that implements word wise uniqueness (see above), but learned Outlines doesn’t support lookarounds. This means even guided outputs can be flawed. Because of the effort required that late in the project, that is expected. Errors in construction will be accounted for in the metrics.

Decoding Settings

Used greedy decoding. Adding in different decoding approaches and additional hyper-parameters could be interesting, but would require more experiments and computations. For now that has been skipped.

Prompt

I used a very simple prompt and didn’t tweak it. While models are brittle, messing around with prompts to improve performance is trivial IMO and falls outstide of the scope of these experiments. The prompt used was:

Click to see code 
You are an expert problem solver. You are doing the "connections" puzzle. You will receive 16 words.

Find groups of four items that share something in common.

Select four items and tap 'Submit' to check if your guess is correct.

Here is an example with 2 groups of 4 fours words

Your words are: Bass;Opal;Trout;Salmon,Ant,Drill,Island;Flounder

Create a JSON with your reasoning and the groups of four found.

{'groups' : [{'theme' : 'FISH', 'words' : ['Bass', 'Flounder', 'Salmon', 'Trout']},
{'theme' : 'FIRE __', 'words' : ['Ant', 'Drill', 'Island', 'Opal']}]}

Categories will always be more specific than "5-LETTER-WORDS," "NAMES" or "VERBS."

Each puzzle has exactly one solution. Watch out for words that seem to belong to multiple categories!

Hyper-parameters (Independent Variables)

Below is the list of hyper-parameters that were varied and their values. The experiment runs essentially a grid search of the following hyper-parameters. See generate_generative_solver_experiments.py.

Models

Tried both llama and the Qwen models. I tried using Mistral models, but they were not supported by Outlines. I used

model_ids = [
    "meta-llama/Llama-3.2-1B-Instruct",
    "meta-llama/Llama-3.2-3B-Instruct",
    "meta-llama/Meta-Llama-3.1-8B-Instruct",
    "Qwen/Qwen2.5-1.5B-Instruct",
    "Qwen/Qwen2.5-3B-Instruct",
    "Qwen/Qwen2.5-7B-Instruct",
    "Qwen/Qwen2.5-14B-Instruct",
]

I didn’t use ChatGPT since it doesn’t have open weights and didn’t feel like spending the money to try this out. Maybe on another iteration, but for now it’s good.

To simplify analysis the number of parameters for a given model will be used instead, rounding to the nearest 500 millionth parameter.

K-Shot

Different k-shot values were used. k_shot_options = [0, 1, 3, 5]

K-shot examples are picked at random from the connections dataset (or sample) excluding the current item and added afterwards.

Click to see code 
if k_shot > 0:
	# TODO: Implement k shot
	examples = nyt_connections_data[:datum_idx] + nyt_connections_data[datum_idx+1:]
	k_shot_examples = random.Random(seed).sample(examples,k_shot)
	for k_shot_example in k_shot_examples:
		k_shot_connections_words = [word for item in k_shot_example['answers'] for word in item['members']]
		formatted_example = {"groups" : [{"words" : group['members'],"theme" : group['group']} for group in k_shot_example["answers"]]}
		messages.append({"role" : "user", "content" : f"Your words are {";".join(k_shot_connections_words)}. Good luck!"})
		messages.append({"role" : "assistant", "content" : json.dumps(formatted_example)})

Guided vs Unguided generation

Tried both guided and unguided generation. use_structured_prediction_options = [True, False]

This is implemented using Pydantic classes.

Click to see code 
AllowedWords = Enum('AllowedWords', {val: val for val in connections_words},type=str)

class Group(BaseModel):
	words: conlist(AllowedWords,min_length=4,max_length=4)
	theme: str

lass ConnectionSolution(BaseModel):
		groups : conlist(Group,min_length=4,max_length=4)

Metrics (Dependent Variables)

A good metric would

  1. Measure how many matches the model got
  2. Be able to account for partial success
  3. Aware of difficulty of a given group
  4. Account for theme accuracy
  5. Detect whether or not an output is valid

The experiments are not turn-based so it excludes certain metrics such as number of turns required to solve, types of errors, model confusion per turn, etc..

Also looking at theme appropriateness, would be interesting but a hard task in its own right. A subjective analysis.

For now two metrics were implemented

  1. mean accuracy, percentage of groups the model got correct. The accuracy could further be segmented based on the difficulty
  2. validity, percentage of inputs that pass the validation regex

Results

Raw Results

Click to see raw results
model_id use_structured_prediction k_shot mean_accuracy percentage_format_passed
meta-llama/Llama-3.2-3B-Instruct False 5 0.06 0.58
Qwen/Qwen2.5-3B-Instruct True 0 0.035 1
meta-llama/Meta-Llama-3.1-8B-Instruct True 5 0.02 1
Qwen/Qwen2.5-1.5B-Instruct False 3 0 0.38
Qwen/Qwen2.5-3B-Instruct False 1 0.04 0.84
Qwen/Qwen2.5-3B-Instruct False 0 0 0
Qwen/Qwen2.5-1.5B-Instruct True 0 0.02 0.98
Qwen/Qwen2.5-14B-Instruct True 3 0.06 1
meta-llama/Llama-3.2-3B-Instruct False 1 0.04 0.42
meta-llama/Meta-Llama-3.1-8B-Instruct False 5 0.06 0.94
Qwen/Qwen2.5-14B-Instruct False 0 0 0
Qwen/Qwen2.5-3B-Instruct False 5 0.015 0.66
Qwen/Qwen2.5-1.5B-Instruct False 5 0 0.48
meta-llama/Llama-3.2-1B-Instruct True 3 0.015 1
meta-llama/Meta-Llama-3.1-8B-Instruct True 1 0.095 1
Qwen/Qwen2.5-1.5B-Instruct False 0 0 0
Qwen/Qwen2.5-3B-Instruct True 3 0.04 1
meta-llama/Llama-3.2-1B-Instruct True 5 0.02 1
Qwen/Qwen2.5-3B-Instruct False 3 0.02 0.86
meta-llama/Llama-3.2-3B-Instruct True 1 0.0555556 1
meta-llama/Meta-Llama-3.1-8B-Instruct True 3 0.065 1
meta-llama/Llama-3.2-1B-Instruct False 5 0.025 0.16
Qwen/Qwen2.5-1.5B-Instruct True 3 0.02 1
Qwen/Qwen2.5-14B-Instruct False 5 0.085 0.84
meta-llama/Meta-Llama-3.1-8B-Instruct False 1 0.16 0.68
Qwen/Qwen2.5-14B-Instruct True 0 0.14 1
meta-llama/Meta-Llama-3.1-8B-Instruct False 0 0 0
Qwen/Qwen2.5-1.5B-Instruct False 1 0 0.2
meta-llama/Llama-3.2-1B-Instruct True 1 0.02 1
meta-llama/Meta-Llama-3.1-8B-Instruct True 0 0.12 0.96
Qwen/Qwen2.5-3B-Instruct True 1 0.05 1
meta-llama/Llama-3.2-3B-Instruct False 0 0 0
meta-llama/Llama-3.2-3B-Instruct True 3 0.01 1
Qwen/Qwen2.5-14B-Instruct False 3 0.07 0.64
Qwen/Qwen2.5-3B-Instruct True 5 0.025 1
meta-llama/Llama-3.2-3B-Instruct True 5 0.01 1
meta-llama/Llama-3.2-3B-Instruct False 3 0.055 0.44
meta-llama/Llama-3.2-1B-Instruct True 0 0.015 0.94
meta-llama/Llama-3.2-1B-Instruct False 0 0 0
Qwen/Qwen2.5-1.5B-Instruct True 1 0 1
meta-llama/Llama-3.2-1B-Instruct False 1 0.005 0.06
meta-llama/Llama-3.2-1B-Instruct False 3 0.01 0.14
Qwen/Qwen2.5-14B-Instruct True 5 0.055 1
meta-llama/Llama-3.2-3B-Instruct True 0 0.065 0.94
Qwen/Qwen2.5-14B-Instruct True 1 0.115 0.98
Qwen/Qwen2.5-1.5B-Instruct True 5 0.005 1
Qwen/Qwen2.5-14B-Instruct False 1 0 0
meta-llama/Meta-Llama-3.1-8B-Instruct False 3 0.08 0.96

Analysis

While there is a limited amount of data (48 points accounting for 3 independent variables over a single task), below are some statistics describing correlations between independent and dependent variables. Two analyses used to measure correlation:

  1. spearman’s rank
  2. coefficient analysis using linear regression
Independent Variable Dependent Variable Correlation P Value
param_count Accuracy 0.531 1e-4
k_shot Accuracy 0.131 0.373
use_structured_prediction Accuracy 0.279 0.055
param_count Validity 0.084 0.561
k_shot Validity 0.301 0.037
use_structured_prediction Validity 0.885 1e-17

Coefficient analysis using linear regression tells a similar story, with the only major difference being that k_shot seems to hurt mean accuracy. Otherwise the relationships, in terms of importance rather than raw values, seems to be the same between coefficients.

Independent Variable Dependent Variable Correlation
param_count mean_accuracy 0.546
k_shot mean_accuracy -0.065
use_structured_prediction mean_accuracy 0.185
param_count percentage_format_passed 0.090
k_shot percentage_format_passed 0.288
use_structured_prediction percentage_format_passed 0.779

There are admittedly confounding variables that aren’t really accounted for within the context of this analysis (# params probably isn’t as meaningful between model families, e.g., 8B Llama3 outperformed Gwen).

Before the experiments my expectation was that increasing any of these hyper-parameters would lead to improved performance. For that reason the most surprising trend was that K shot seems to have a very limited impact on performance. I’m not sure if this reflects a true trend or an issue with the experiment such as the setup or inappropriate statistical techniques. With more data an interesting analysis would be multi-variable correlation analysis, for example if smaller models benefit more, if at all, from higher values of K in K-shot. Difficulty aware performance would also be interesting, are models only solving easy groups or is there no particular trend?

Conclusion and Next Steps

Current results are rather poor, with the best model getting only 16% (30/192) of the groups correct. While there are tweaks that could be done to the experiments above such as:

  1. Use of ChatGPT
  2. Higher values of K
  3. Use of a regex for guided generation (requires a different library or custom code
  4. Prompt optimization, likely not manually but rather through use of prompt optimization tools like DSPy or TextGrad

I would rather focus on fundamentally different approaches that are more efficient and potentially leverage data structures to solve the problem.

Next attempt will likely be a combination of framing the problem as classification (whether two or more words are related) and use of a dynamic programming algorithm to pick which groups of four is most likely, potentially with additional checks for validity. This would enable batching and potentially even use of smaller models. It might also be an interesting opportunity to analyze how word usage is captured by a given representation.

<
Previous Post
Quick and Dirty Metric to Imperial Conversions (How to Entertain Yourself as an American Driving in a Metric Country)
>
Next Post
Fun with Words: A Foray into Solving NYT Connections via Decomposition